In this article, let’s learn about flip flop conversions, where one type of flip flop is converted to another type.
For the conversion of one flip flop to another, a combinational circuit has to be designed first. If a JK Flip Flop is required, the inputs are given to the combinational circuit and the output of the combinational circuit is connected to the inputs of the actual flip flop. Thus, the output of the actual flip flop is the output of the required flip flop. In this post, the following flip flop conversions will be explained.
- SR Flip Flop to JK Flip Flop
- JK Flip Flop to SR Flip Flop
- SR Flip Flop to D Flip Flop
- D Flip Flop to SR Flip Flop
- JK Flip Flop to T Flip Flop
- JK Flip Flop to D Flip Flop
- D Flip Flop to JK Flip Flop
As told earlier, J and K will be given as external inputs to S and R. As shown in the logic diagram below, S and R will be the outputs of the combinational circuit.
The truth tables for the flip flop conversion are given below. The present state is represented by Qp and Qp+1 is the next state to be obtained when the J and K inputs are applied.
For two inputs J and K, there will be eight possible combinations. For each combination of J, K and Qp, the corresponding Qp+1 states are found. Qp+1 simply suggests the future values to be obtained by the JK flip flop after the value of Qp. The table is then completed by writing the values of S and R required to get each Qp+1 from the corresponding Qp. That is, the values of S and R that are required to change the state of the flip flop from Qp to Qp+1 are written.

This will be the reverse process of the above explained conversion. S and R will be the external inputs to J and K. As shown in the logic diagram below, J and K will be the outputs of the combinational circuit. Thus, the values of J and K have to be obtained in terms of S, R and Qp. The logic diagram is shown below.
A conversion table is to be written using S, R, Qp, Qp+1, J and K. For two inputs, S and R, eight combinations are made. For each combination, the corresponding Qp+1 outputs are found ut. The outputs for the combinations of S=1 and R=1 are not permitted for an SR flip flop. Thus the outputs are considered invalid and the J and K values are taken as “don’t caresâ€.

As shown in the figure, S and R are the actual inputs of the flip flop and D is the external input of the flip flop. The four combinations, the logic diagram, conversion table, and the K-map for S and R in terms of D and Qp are shown below.

D is the actual input of the flip flop and S and R are the external inputs. Eight possible combinations are achieved from the external inputs S, R and Qp. But, since the combination of S=1 and R=1 are invalid, the values of Qp+1 and D are considered as “don’t caresâ€. The logic diagram showing the conversion from D to SR, and the K-map for D in terms of S, R and Qp are shown below.

J and K are the actual inputs of the flip flop and T is taken as the external input for conversion. Four combinations are produced with T and Qp. J and K are expressed in terms of T and Qp. The conversion table, K-maps, and the logic diagram are given below.

D is the external input and J and K are the actual inputs of the flip flop. D and Qp make four combinations. J and K are expressed in terms of D and Qp. The four combination conversion table, the K-maps for J and K in terms of D and Qp, and the logic diagram showing the conversion from JK to D are given below.

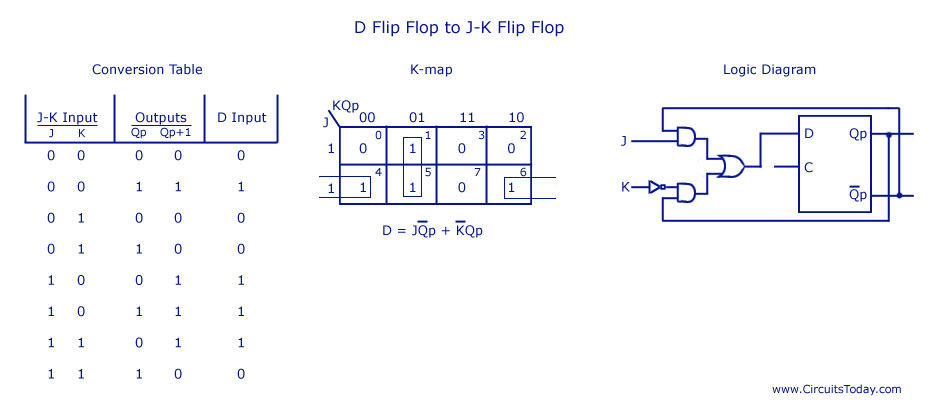
In this conversion, D is the actual input to the flip flop and J and K are the external inputs. J, K and Qp make eight possible combinations, as shown in the conversion table below. D is expressed in terms of J, K and Qp.
The conversion table, the K-map for D in terms of J, K and Qp and the logic diagram showing the conversion from D to JK are given in the figure below.

Best Helping Materials Regarding with Flip Flop Conversion 🙂
Thank You Sir 🙂
How to convert JK ff to D ff on digital traineer kit?How to convert D ff to JK ff on digital traineer kit?
how to convert JK ff to D ff on digital traineer kit?
If we are designing the JK flip flop using SR flip flop ,In that case what is the role of K-map in that designing procedure
Very usefull ,but a small mistake is there in jk to d
In d flip-flop when D=1 Q(p+1)=1
thanks sir it is very clear and understandable . i am confuse convert JK flip flop to T flip flop when i solve this the answer of this is comes J=T and K=T zabar but you are answer is different
Can you do the charateristic table for the converted gate? What will be the charatersitic table for ‘JK Flip-flop to T flip-flop’ circuit for example?
still more flip flop conversions must be there
there is mistake in D flip-flop to JK flip-flop
there is a mistake in the SR flipflop to JK flipflop where S=(~J)*Qp.
I agree, There is AN ERROR. JK —> SR. It is suppose to be S= JQ’
yeah, encountered the same thing. there’s a mistake there in the first conversion.
THANKS
How to convert sr flip flop to t flip flip?
In conversion of sr to jk flipflop
Y r we not paring with don’t cares..???
Since we are pairing with don’t cares in each conversion…
Reply me on my mail id its urgent to know…
Thanks
very helpful……. great job
this is awsome.it is very helpfull to me for checking my task is correct or not……..thanks a megaton
yeah this is very helpful
but one mistake is there.in SR toJK flip flop the eqn for s will be S=J*Qp bar .
very easily explained.Thanks a lot
Very helpful….i clear this topic..
it is very useful 4 me thanks for u
Wonderful explanation. Easy language used. Very easy to learn! Thanks a ton!
Its very clear and understandable , thank u so much.
It will be S=J*(Q_p)’ in S-R to J-K conversion instead of J’*(Q_p) this error is in the K-Map Solution for S.
Otherwise it is very good content and very useful..
Thanx
it is very useful to me thanks………….
These information are very helpful for those who want to know about flip flop. It is wonderful.
This was wonderful. I am going to tell my classmates about it. Our professor just couldn’t seem to explain it this clearly, so this really helped. Thanks!
In the SR Flip Flop to D Flip Flop
there is a mistake in the R K-Map
the term (1) should be “1” not “0”
found it helpful for writing exam …
ACTUALLY COYING DURING THE EXAM 😀
KEEP IT UP !!!!!!!
thank you so much my exam’s in 4 hours i needed this
Awesome. Thanks. Althought there’s an error on the JK Flip Flop to D Flip Flop table. Last line. Qp+1 should be 1 and not 0. But the corresponding JK Inputs are correct. This said, everything is good except Qp+1.
Thanks A bunch…:-)
was really helpful…….thanks a bunch
That Was awesome….gracias…
please try to keep the solution for D-ff to T-ff conversion
can i have details about D flip flop to SR flip flop using NOR gates only.
when an SR is clocked it dxnt matter whether its NOR or NAND…. both have same characteristics….
muy buen contenido …gracias
thank u very much…!!
its up to the point and brief.
very helpful.thankyou
simply awsom…..helpfull…
Very useful! Thank u very much!
thankyou so much!!!
Thank you so much…Saved me 🙂
Thanks a lot
This is nice site for digital logic
Thank’s you so much it is good details for digital information. i will com back in your web sites.
Thanks a lot
I hope if there is a suitable reference (student language not complex teacher language methods) for digital communication and for digital system design ??
its so so interesting & excellent
This is very interesting…
thanks
Alireza
I worked in the Postal Service, it had a large training section where we laearned to service electronic equipment. It was located in Norman, Oklament. At the University of Oklahoma. The last equipment I woked on was the Optical Cahriter Reader (OCR) the hardest logic I had to learn was the Master Slave J K Flipflop. I finnaly learned how it worked just before the test that was given every Friday. Well that was the only question I missed on the test. The instructor had a way to change just a little of something different.
thank u 🙂
good one and thanks dude for help me for this topic ………
Thanks a lot. It will help to brush up my skills.
Excellent!!!
very helpful
Perfect !
Now I think i can convert any flip flop to other !
Thanks a lot !
the figure in the conversion of jk to d is slightly incorrect …
the last row in the conversion table should be corrected…i feel ….
please comment if i am wrong…
you are correct, the last row should be qp = 1 and qp+1 = 1
yes
d=1 Qp=1 Qp+1=1
thank you very much.the explanations is quite simple and very easy to understand.please also post on registers.
Excellent! Thank you very much.
very good.explanation is quite simple and fundamentally stupedous
Excellent!
Thank you.
Thank you very much john. Much needed topics!!
you worked really hard Mr. john. You concentrated upon a very useful topic.
Excellent!
Thank you so much!