In this article, learn about Ripple carry adder by learning the circuit. A ripple carry adder is an important digital electronics concept, essential in designing digital circuits.
Ripple carry adder circuit.
Multiple full adder circuits can be cascaded in parallel to add an N-bit number. For an N- bit parallel adder, there must be N number of full adder circuits. A ripple carry adder is a logic circuit in which the carry-out of each full adder is the carry in of the succeeding next most significant full adder. It is called a ripple carry adder because each carry bit gets rippled into the next  stage. In a ripple carry adder the sum and carry out bits of any half adder stage is not valid until the carry in of that stage occurs.Propagation delays inside the logic circuitry is the reason behind this. Propagation delay is time elapsed between the application of an input and occurance of the corresponding output. Consider a NOT gate, When the input is “0” the output will be “1” and vice versa. The time taken for the NOT gate’s output to become “0” after the application of logic “1” to the NOT gate’s input is the propagation delay here. Similarly the carry propagation delay is the time elapsed between the application of the carry in signal and the occurance of the carry out (Cout) signal. Circuit diagram of a 4-bit ripple carry adder is shown below.

Sum out S0 and carry out Cout of the Full Adder 1 is valid only after the propagation delay of Full Adder 1. In the same way, Sum out S3 of the Full Adder 4 is valid only after the joint propagation delays of Full Adder 1 to Full Adder 4. In simple words, the final result of the ripple carry adder is valid only after the joint propogation delays of all full adder circuits inside it.
Full adder.
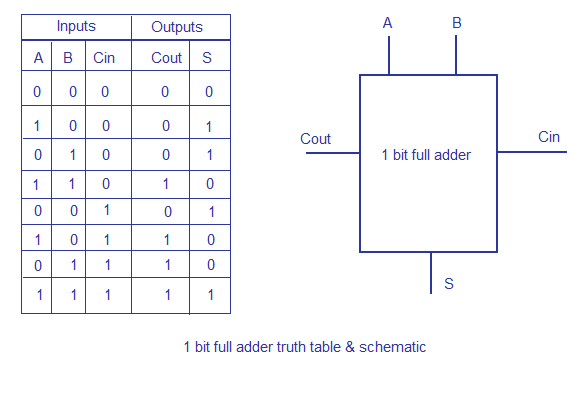
To understand the working of a ripple carry adder completely, you need to have a look at the full adder too. Full adder is a logic circuit that adds two input operand bits plus a Carry in bit and outputs a Carry out bit and a sum bit.. The Sum out  (Sout) of a full adder is the XOR of input operand bits A, B and the Carry in (Cin) bit.  Truth table and schematic of a 1 bit Full adder is shown below
There is a simple trick to find results of a full adder. Consider the second last row of the truth table, here the operands are 1, 1, 0 ie  (A, B, Cin). Add them together ie 1+1+0 = 10 . In binary system,  the number order is 0, 1, 10, 11……. and so the result of 1+1+0 is 10 just like we get 1+1+0 =2 in decimal system. 2 in the decimal system corresponds to 10 in the binary system. Swapping the result “10” will give S=0 and Cout = 1 and the second last row is justified. This can be applied to any row in the table.
 A Full adder can be made by combining two half adder circuits together (a half adder is a circuit that adds two input bits and outputs a sum bit and a carry bit). Â

Full adder using NAND or NOR logic.
Alternatively the full adder can be made using NAND or NOR logic. These schemes are universally accepted and their circuit diagrams are shown below.



send the cmos level circuit of 4 bit ripple carry adder
HOW To make a 7:5 ripple carry addder
to given truth table
what actully a ripple carry addder is…?
How to 8 bit encryption logic gates.
I believe the full adder truth table image file is wrong in the last row.
Should not Cout and S both be TRUE when inputs A,B, Cin are all TRUE?
I’ve included the URL for the full adder truth table file
https://circuitstoday.com/wp-content/uploads/2012/03/i-bit-fill-adder-truth-table_schematic.png
Hello Melton 🙂
Thanks for notifying us. We corrected it 🙂
hahaha. sab haule hai 😛
hi,
actually you have not understood the TT of Full adder,
when A=1, B=1,Cin=1 it implies sum is 3 and it’s binary form is 11.so,we will have to write S=1 and Cout=1
please go through some standard book like marris mano.