Bubble sorting is one of the simplest sorting algorithm that we can use to sort an array or a structure. Though it is so simple to implement in a C program, bubble sort is also considered as an inefficient sorting algorithm. Bubble sort comes handy in cases where the total number of elements to be sorted is so small (may be in the 100’s range). When the data size is large/huge bubble sort is seldom used in practical programming world. Let’s analyse bubble sort algorithm in detail by implementing it as a C program.
Note:– Since the algorithm is implemented with the help of 2 FOR loops only, it can be used as such for any programming languages like C/C++ or Java
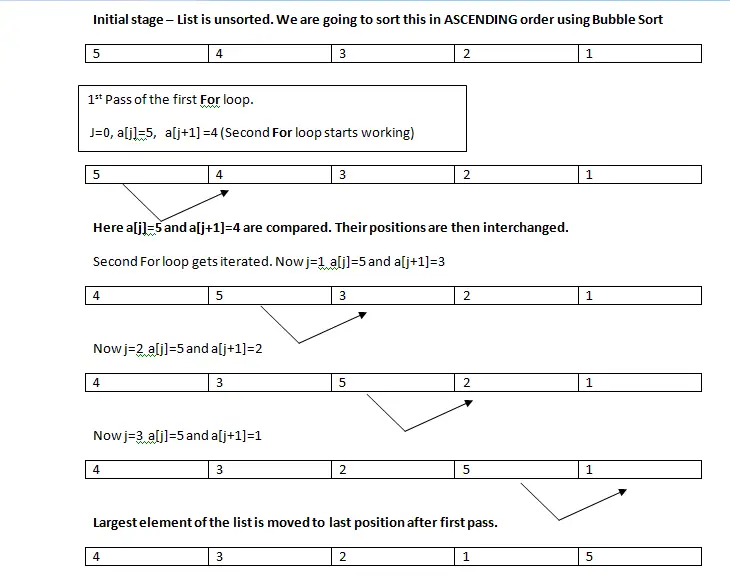
The working of Bubble sort:-
Consider an array of 5 elements in the order 5 , 4 , 3 , 2 , 1. We need to sort this list in ascending order using bubble sort. The concept of bubble sort algorithm is simple, we can explain it in 2 steps.
For the simplicity of explanation, I am going to consider sorting in ascending order.
- Step1:- The first member of the list is compared with the next element. To sort in ascending order we usually begin the process by checking if first element is greater than next element. If yes, we interchange their position accordingly. i.e first element is moved to second element’s position and second element is moved to first element’s position. If No, then we dont interchange any elements. As next step, the element in second position is compared with element in third position and the process of interchanging elements is performed if required. The whole process of comparing and interchanging is repeated till last element. When the process gets completed, the largest element in array will get placed in the last position of the list/array.
- Note 1 for Step 1:- Here the point to note is that, we compare two elements in succession i.e we compare 1st and 2nd element – then 2nd and 3rd element – then 3rd and 4th and finally 4th and 5th. So the total number of comparisons is 4 (for an array/list of 5 elements). If there are ‘n’ elements to be sorted, then the total number of comparisons to be made is = n-1
- Step 2:- The whole process in step 1 is repeated 5 times to get the sorted array in order 1 , 2 , 3 , 4 , 5. If there are n elements to be sorted, the whole process of step 1 is repeated ‘n’ times.
for(i=0; i
{
temp=a[j]; // The 3 following statements are used to interchange positions of compared elements.
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
 Now you can easily find the efficiency of “Bubble Sort” algorithm. If there are ‘n’ elements, it is of the order of n*n. This is simply because it takes nearly n comparisons to be made n times.
Now you can easily find the efficiency of “Bubble Sort” algorithm. If there are ‘n’ elements, it is of the order of n*n. This is simply because it takes nearly n comparisons to be made n times. Modifying the Bubble sort:-
for(i=0; i
{
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
With this new modified code, we can improve the speed of bubble sort.
The best case and worst case scenarios of Bubble sort:-
The best case is when the algorithm gives its maximum efficiency (and fast performance) where as the worst case is when it gives the least efficiency (slowest performance). In the case of Bubble sort, the best case is when the array to be sorted is in the perfect order(in the sorted order). Example:- Take the case of an array in the following order 1 , 2, 3, 4, 5 and we need to sort it in ascending order. In this case the array is already sorted! So when implementing this with bubble sort, the sorting algorithm only makes comparisons. There is no interchange of elements happening any time while the algorithm works. Thus bubble sort performs in its maximum efficiency and requires only minimum time. The worst case of bubble sort is when we need to sort an array arranged in descending order to be sorted in ascending order or vice versa. Consider the case of an array in order 5, 4, 3, 2, 1 and we need to use bubble sort to sort this array in ascending order. In this case the algorithm makes maximum number of comparisons along with maximum number of element exchanges. Hence the algorithm gives its worst performance (takes maximum time)
Improving the algorithms performance in C
Many cases/scenarios can occur when we analyse a sorting algorithm. Just like the best case and worst case scenarios. In best case scenario of sorting an array 1, 2, 3, 4, 5 we have seen that there is “no exchange of elements” happening any time (through out the working of algorithm). Now consider another scenario of sorting an array of order 1, 2, 3, 5, 4; Here only the last 2 elements are not in order, where as the first 3 elements are in order. According to bubble sort algorithm, the largest element will occupy last position after completing first pass of loop. That means, after the first pass, the array will become 1, 2, 3, 4, 5 – and it gets sorted. So in this case the remaining 4 passes made by first FOR loop is a waste of time. After the first pass, only comparison of elements will take place and there will be no “exchange of elements”.
From this analysis, we can arrive at a conclusion. If a particular pass (say 3rd pass) of loop resulted in “no exchange of elements” through out that particular pass, then we can assume that, the array is already sorted. Thus we can skip the rest of passes through loop by giving a break statement or using a flag. By doing this we are saving a lot of time that might have got lost in unnecessary looping. This modification can be implemented using the following code snippet.
for(i=0; i
{
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
flag=0; // flag is set back to zero because there occured an "exchange of element"
}
}
}
Hope you have understood the “bubble sort” algorithm well enough. If you have any doubts, please ask in comments section.

#include
int main(){
int s,temp,i,j,a[20];
printf(“Enter total numbers of elements: “);
scanf(“%d”,&s);
printf(“Enter %d elements: “,s);
for(i=0;i=0;i–){
for(j=0;ja[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
printf(“After sorting: “);
for(i=0;i<s;i++)
printf(" %d",a[i]);
return 0;
}
pls clear the loop
#include
int main(){
int s,temp,i,j,a[20];
printf(“Enter total numbers of elements: “);
scanf(“%d”,&s);
printf(“Enter %d elements: “,s);
for(i=0;i=0;i–){
for(j=0;ja[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
printf(“After sorting: “);
for(i=0;i=0;i–){
for(j=0;ja[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
please clear it.
thank you
Good Explanation dude keep it up.
Awsome!! it helped me alot!! :p
i am unable to get use of flag variable here…can u little bit explain the flag variable concept in this code????
Plz…..continue writing article over c tutorial !!! It helps a lot to beginner like me !!